This blog was last modified 422 days before.

In this post we are going to discuss the how the floating numbers stored in computer.

Most of current computer system comply with IEEE 754 , which is an international standard to store such floating point number into computer.

How to use this post?

This post is a complement and extra explanation, it's recommend that you check out the IEEE 754 Wikipedia Page first.

And when you find some hard-to-understand conceptions and mechanisms, back to check if this post has some extra content can help you.

Structure

As the name imply, floating point means the decimal point could floating , and this floating is produced by the mutate the exponent part.

2.30e2
2.30e3 = 23.0e2

In above example, you can imagine the decimal point shift right.

In case some readers don't know, e[x] here means 10^x, for example, 2.3e3 means 2.3*10^3. e here represents Exponent .

In IEEE 754 , a floating point comprise 3 parts:

• Sign
• Exponent
• Fraction

A simplified sturcture diagram could like the image below:

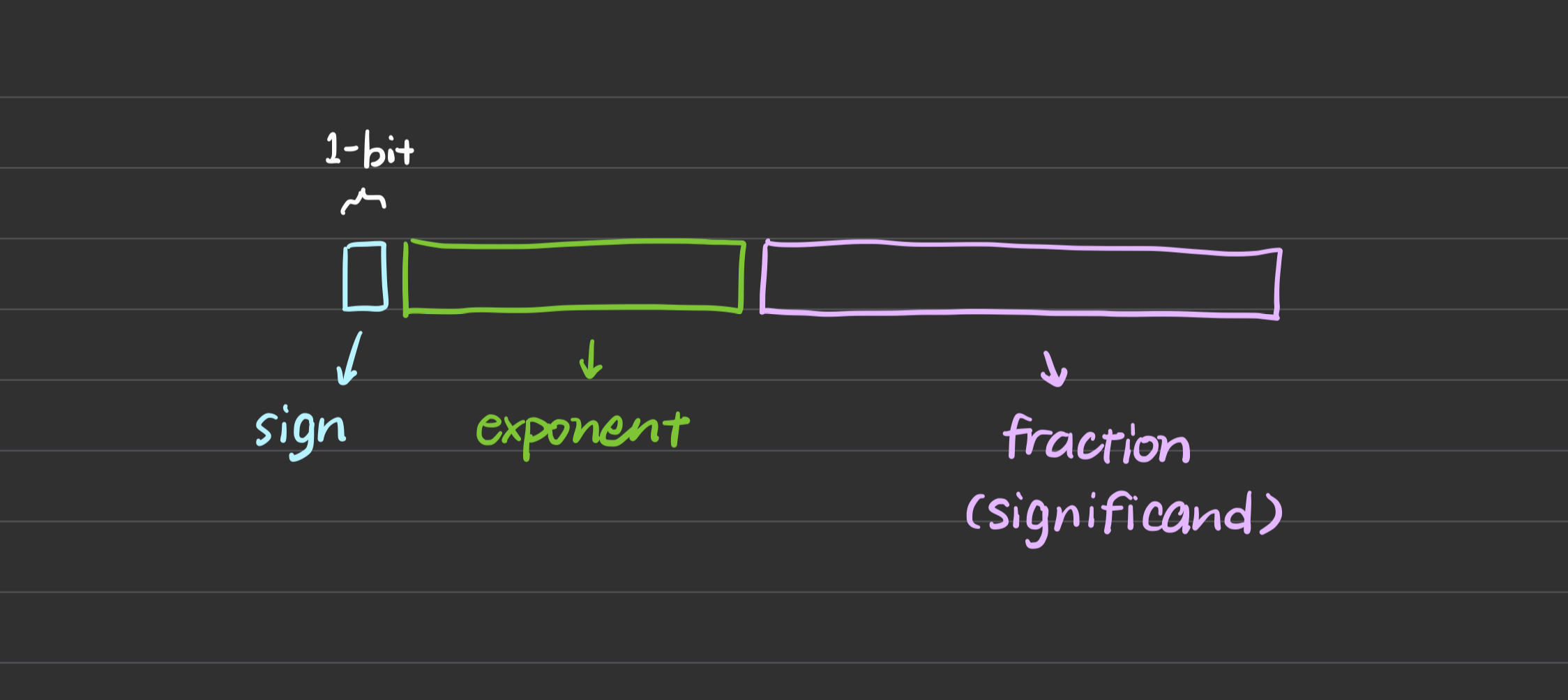
There are both standard to store binary floating number and decimal floating number, and their mechanism is the similar. For convenience, the following post will take binary floating number as example.

Patterns

• sign Always 1 bit. 0 represents positive, 1 represents negative.
• exponent & significand Varys from different type of floating point number.

Bias for exponent

As you see from the picture above. For n-bits exponent, its bias is $2^{n-1} -1$ .

More directly, if there is an 7-bits exponent ???????, then its bias is 0111111.

The value in memory, bias, and the actually represented value has following relationship:

Check the example picture below: (In which Org means the value in storage/memory, the middle column means bias, and the right column means the actual represented value)

Special Cases

• All Zeros. This represents subnormal numbers in the standard. And which means hidden one convention will be disabled.
• All Ones. This indicates infinity or NaN . Check Wikipedia for more info.

Hidden One Convention for significand

As you see, when we representing the normal numbers (in the normal range of the standard), then we could always expected that the first bit in the significand of the number is 1. So we could just ignore this 1, which could help us save one bit. (Notice this convention doesn't work when we are representing numbers in the subnormal ranges).