这篇文章上次修改于 708 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
Binary Coded Decimal
I guess most of you guys have already quite familiar to this concept, and it has another name 8421 code in some textbooks.
Basically it just means use a nibble (4-bits) to represents a number in decimal. Check Binary Coded Decimal Introduction for more info.
For example, the decimal number 32 will be 00110010b in BCD, if you use hex to represent it, it would be 32H.
Now take times to practice the convertion yourself, and think about why the hexadecimal representations looks quite similar to the original decimal form.
Correction of BCD Calculation
Now do you remember we said there is a flag called Auxiliary Flag in 8086 CPU? That's actually dedicated for BCD calculation.
BCD Addition Correction
Consider how machine add up two numbers. Let's assume we need to add up two numbers: 18 (18h in BCD) and 7 (07h in BCD).
mov al, 18h
mov bl, 07h
add al, blNow the value in al will be 1fh. Appearantly it's not a valid BCD encode.
Why this error occured? Because when we doing addition in decimal, we would round up when the number reach to 10. But that's not the case in BCD.
09 + 01 = 10
09h + 01h = 0ah
09 + 03 = 12
09h + 03h = 0chSo how can we fix this? Just check it manually.
First: Check whether the lower nibble (for example the c in 0ch) is greater than 9 (Or AF==1). If it is:
- Add the lower nibble by 6.
AF = 1.
Second: Check the whether AL > 9fh (Or CF==1). If it is:
AL = AL + 60h.CF = 1.
Notice the two step of check are both used some flags, why we need this flags? Check the pic below:

What does Auxiliary Register Actually Do?
When calculating some BCD numbers like 99h + 99h, we will get a result of 32 (actually 132 but the round up do not stored in the register but use the carry flag CF to represent). When we check about 32, we found that the number 2 doesn't greater then 9, and 32 itself doesn't greater then 9fh.
However the lower nibble is 2 doesn't means it doesn't need correction. It could be 0+2=2 (HEX), but it also could be 9+9=12 (DEX). So it's not enough to only check the number, we need a register to record that whether there is a rounding that we can't detect through solely check the value in the lower nibble when adding up lower nibble, and that is what AX do.
Reading the description maybe a little adstract, let's do experiment!
I wrote a program (Here is Source ASM Code) to check when the AF has been set to 1 (We said before the AF could not be directly read, so I use some trick and you can check the code for more info). And I got result below:
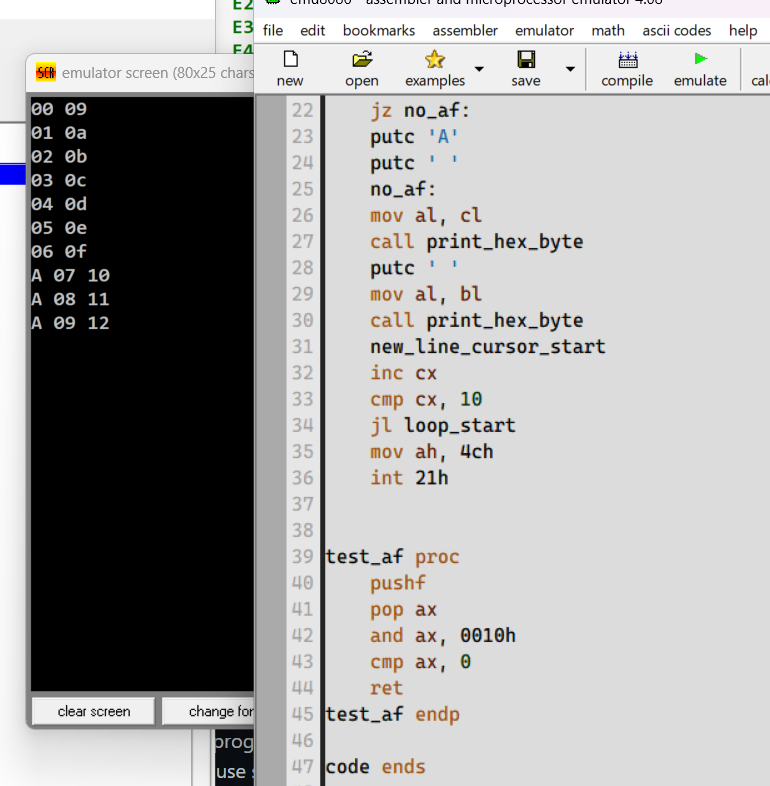
Note:
- Number showed in hexadecimal.
- Doing
9+x, in whichxis from 0 to 9 - The first printed number is
x, the second number is the result of the addition. - If there is an
A, meansAF=1after this addition.
Now you know, when the result of the addition of the two lower nibble is greater than 0f (in which situation we can't know if we need to correction only based on the result of the lower nibble), then the AF will be set to 1.
BCD Substraction Correction
Similar to addition correction. Check 8086 Instruction Manual for more info about the correction of BCD calculation.

没有评论